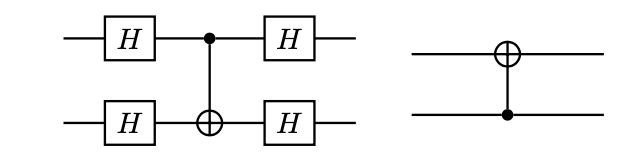
定义生成矩阵
G=0011010101111001101111011111
称它的行向量构成的空间为 C,包含 16 个码字。它的补空间是
C⊥={x∣x⋅c=0∀c∈C}
对应的生成矩阵是
H=001010011100101110111
它们具有性质 GHT=0。
一个码 C 如果码字间最小的非零距离是 d,那么码可以校正 t=(d−1)/2 个错误,检出 d−1 个错误。
编码过程
将 m 编码为 mG
解码过程
设收到的信息为 r=mG+e,则
rHT=(mG+e)HT=eHT
则结果对应于 HT 的某一行,通过这个信息可以得出 e。
编码过程
∣0⟩L=81c∈H∑∣c⟩
∣1⟩L=81c∈H∑∣c⊕1111111⟩
解码过程
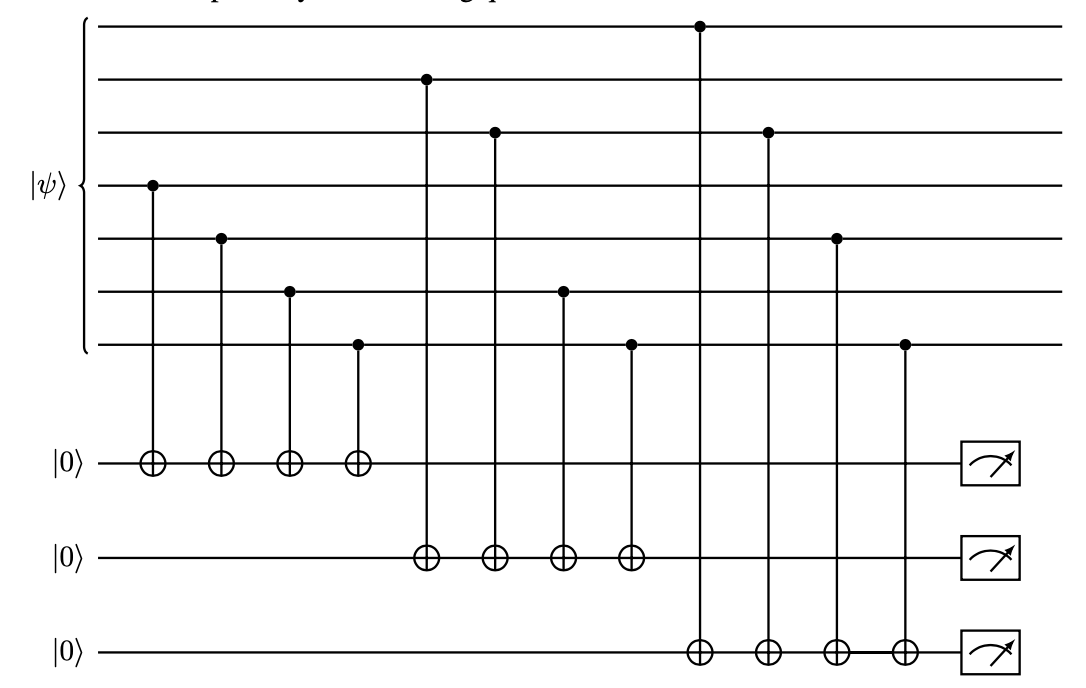
计算特征:
(b4⊕b5⊕b6⊕b7,b2⊕b3⊕b6⊕b7,b1⊕b3⊕b5⊕b7)
可以判断出哪个位出现翻转错误。类似地,由于这种码对 n 元 Hadamard 变换具有不变性
H⊗7∣0⟩L=21(∣0⟩L+∣1⟩L)
H⊗7∣1⟩L=21(∣0⟩L−∣1⟩L)
同理,一个逻辑的 σx 即是 σx7,σz 也是如此。
符号翻转错误可以用两种方式